数字信号由来及发展

数字逻辑起源于19世纪，1847年，逻辑代数的创始人——英国数理逻辑学家Boole（布尔）发表了1篇关于符号逻辑的论文。19世纪50年代，他又运用代数方法研究逻辑学，成功地建立了第1个逻辑演算，引出数学当中的1个分支——布尔代数；1938年克劳德·香农（Claude E.Shannon）发展了布尔的理论，形成了数字电路分析、设计的一整套理论，这就是布尔代数。布尔代数是用数学符号描述逻辑处理的一种逻辑形式，也称逻辑代数，又叫开关代数。从20世纪初的电子管，50年代贝尔实验室发明的晶体管，到60年代的集成电路（IC），以及70年代的微处理器，随着电子器件的发展，电子整机设备的发展非常迅速，其发展趋势是：向系统集成、大规模、低功耗、高速度、可编程、可测试、多值化等方面发展。

模拟/数字信号

在自然界中，存在着两类物理量：一类称为模拟量（Analog Quantity），它具有时间和数值都连续变化的特点，例如温度、压力、交流电压等就是典型的模拟量；另一类称为数字量（Digital Quantity）

模拟量/Analog Quantity

时间和数值都连续变化，例如：温度、压力、交流电压等

数字量/Digital Quantity

时间和数值上都离散变化

数字电路

数字电路中数字信号的取值只有0和1，用0和1描述两种完全对立的状态，绝对没有第3种取值

数字信号1个0或1的持续时间称为1拍，即比特(bit)。

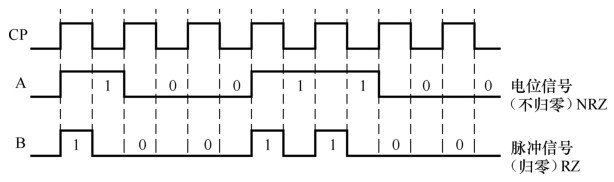
数字信号的有两种传输波形：电位型和脉冲型

电位型数字信号

以一个节拍内信号是高电平还是低电平来表示1或0，也称为不归零型(Non-Return-Zero,NRZ)数字信号

脉冲型数字信号

以一个节拍内有无脉冲来表示1或0，也称为归零型(Return-Zero,RZ)数字信号

数字电路的特点

以数字量的形式处理信息的优点如下：

精度高:
- 只要设备量允许，可以做到很高的精度,比如13位二进制的器件就可以有8192个间隔，使数字量和模拟量对应
- 在数字电路的基本单元电路中，对元件精度要求不高，允许有较大的误差，只要电路在工作时能可靠区分0和1两种状态即可
可靠性高: 因为传递、记录、加工的信息只有0和1，不是连续变化，所以由数字电路组成的数字系统，抗干扰能力强，可靠性高，精确性和稳定性好
容易处理信息：可以方便的对信息进行存储、算术运算、逻辑运算、逻辑推理和逻辑判断
保密性：数字量在进行传递时可以加密处理
快速：单个晶体管的开关时间可以小于10皮秒(1皮秒=1微微秒=10-12秒)
经济型：电路结构简单，制造容易，便与集成和系列化生产，价格低，使用方便。

数字集成电路的分类

把由各种器件(包括二极管、三极管、电阻等原件)及布线连接成的各类电路制作到一个很小的半导体基片上所构成的电路，叫集成电路(Integrated Circuit,IC),集成电路可分为数字集成电路和模拟集成电路
数字集成电路主要有：体积小、功耗低、可靠性高等特点

按照集成度大小，数字集成电路可分为：

小规模集成电路(Small Scale Integrated Cricuit,SSIC)：逻辑门数目介于10~99;
中规模集成电路(Medium,MSIC):逻辑门数目介于100~999;
大规模集成电路(Large,LSIC):逻辑门数目介于1000~9999;
超大规模集成电路(Very Large,VLSIC):逻辑门数目超过10000;

摩尔定律: 由戈登摩尔于1965年提出，主要内容：集成电路最小特征尺寸以每三年减小70%的速度下降，集成度每18个月翻一番;价格每两年下降一半;这种规律在30年内是正确的(从1965年开始)

按照应用，数字集成电路可分为：

通用型集成电路，指已被定型的标准化、系列化的产品，适用于不同的数字设备;
专用型集成电路，指为某种特殊用途专门设计，具有特定的复杂而完整功能的功能块型产品
可编程逻辑器件(Programmable Logic Device,PLD)，指由用户编程以实现某种逻辑功能的新型逻辑器件

按照有源器件及工艺类型的不同，集成电路可分为：

双极型晶体管集成电路
单极型MOS集成电路
双极与MOS混和集成电路